Fourier's Finches: A Primer on Digital Audio
As far as I know, Jean-Baptiste Joseph Fourier never took an interest in birds, but he was a legendary mathematician who’s work enabled our modern techniques for digital audio. Fourier discovered a mathematical transformation that converts a time signal into a frequency signal. This would let us, for example, record a finch’s birdsong and decompose it to find the major frequencies. This would be useful for compressing the audio file. By studying the anatomy of the ear, you can throw away all the frequencies that the ear wouldn’t hear anyway. This same technique generalizes to digital image compression too.

Let’s start with a house finch, here’s what one might sound like:
The Fourier Transform takes the time signal, a function \( f(t) \), and transforms it to the frequency signal using this integral:
$$ \hat{f}(\omega) = \int^{\infty}_{-\infty}f(t)e^{-2\pi i\omega } dt $$
The \( e^{ix} \) function is deeply connected to circles, to understand why, see my earlier post. The integral is like a continuous addition of a bunch of infinitesimal slices. So imagine summing over a bunch of time slices, all spaced out by \( \omega \). This sweeps over the whole time signal and then allows you to decompose the signal into frequencies. If you take this Fourier transform of the house finch file, it looks like this:
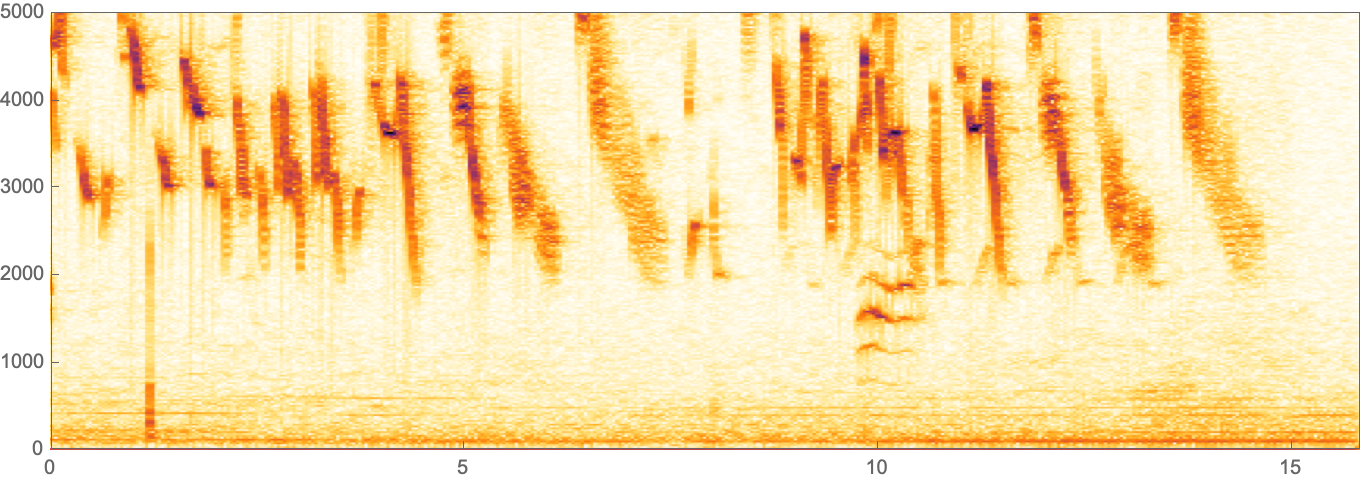
So this view of audio data will allow you to compress the file and save a lot of space without losing too much quality. Once you throw away the frequencies that the ear can’t hear, then you invert the transform to get a time signal that now takes less information to store.
What’s the actual structure of the WAV file? The first 44 bytes of the file are the header, which contains metadata like this:
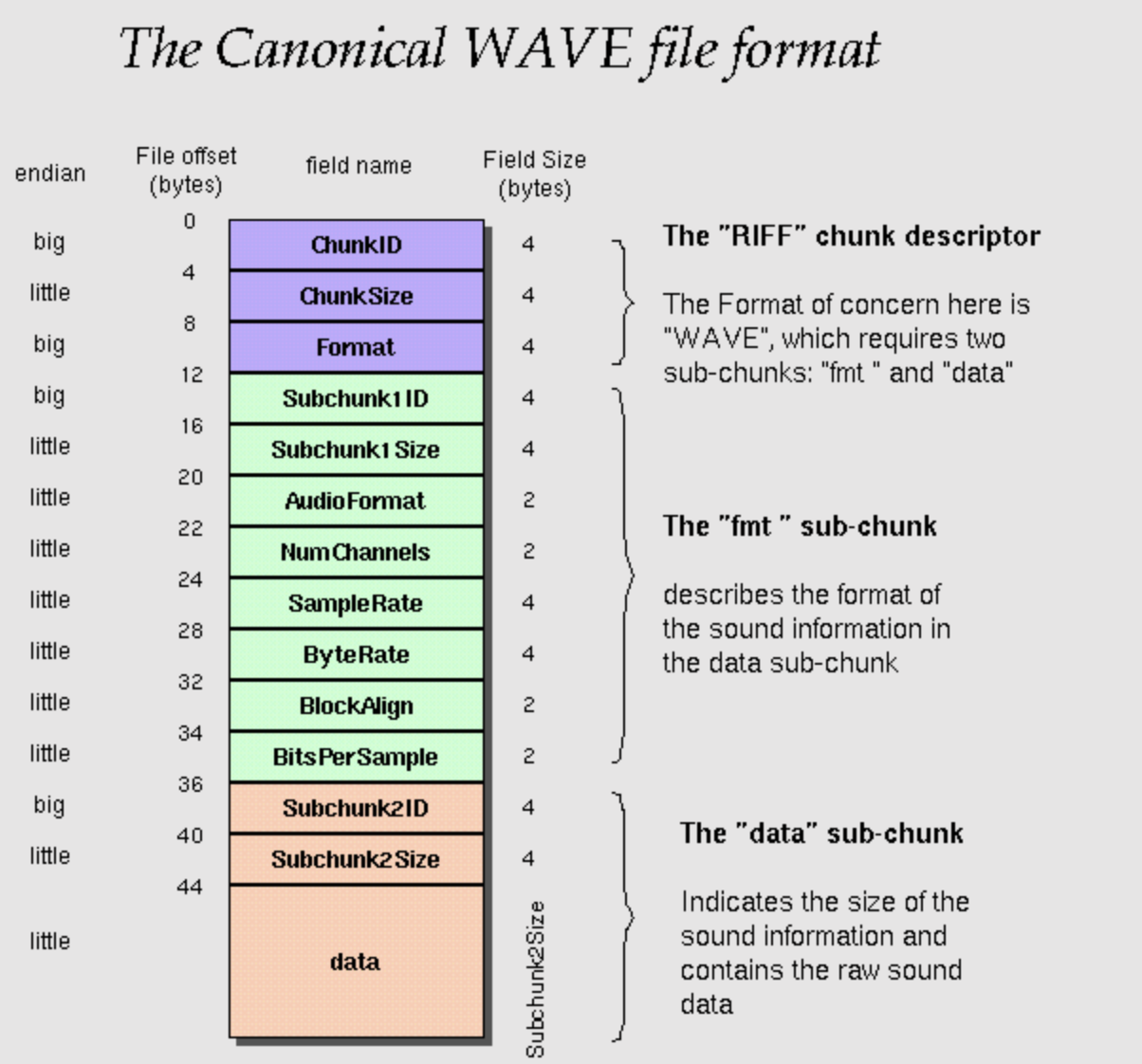
In the data sub-chunk, the discretized samples of the waveform are stored as floating point numbers. They are literally the \(f(t)\) values. If the file is a stereo file, then the samples are interleaved.