Literate Quicksort

This post is a literate program, it both explains and implements quicksort. Quicksort is a fast, recursive sorting algorithm. The big idea is to take an array of \( n \) unsorted integers, choose a pivot element, and then recursively sort the two arrays on either side of the pivot.

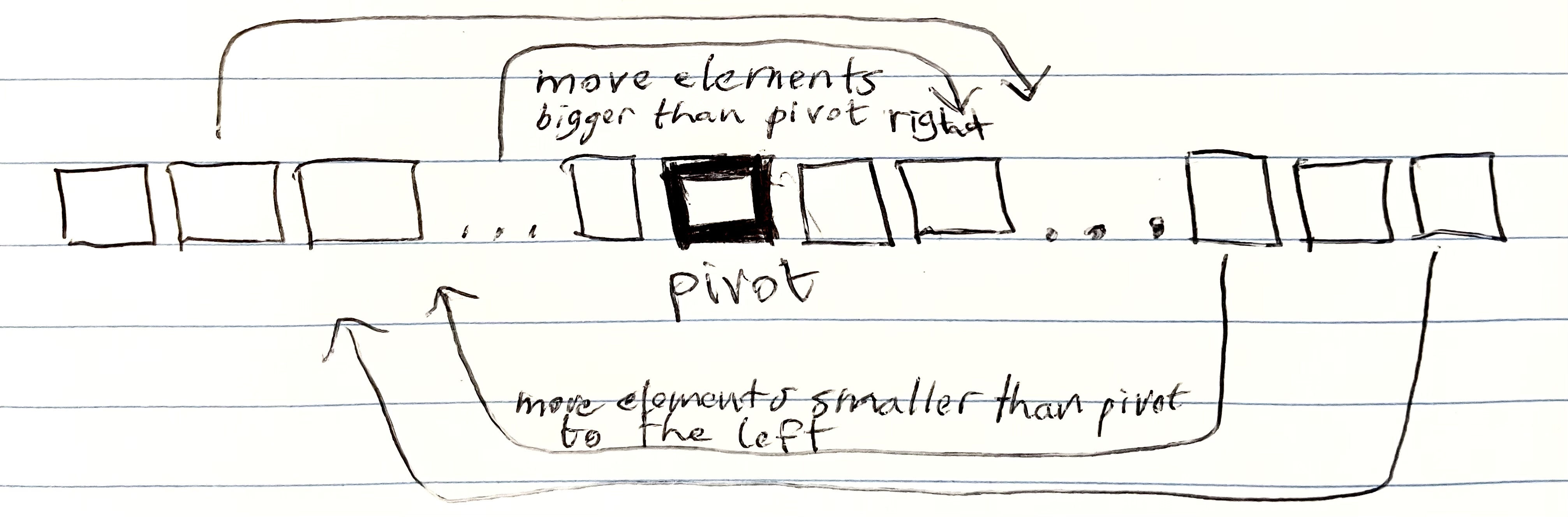
Once a pivot is selected, every number to the left of the pivot is smaller, and every one to the right is bigger. This pivot selection process is called partitioning, since it creates two partitions which can be sorted independently. The pivot is already in it’s final sorted place.

Here’s an example of partitioning, I made this animation from these excellent slides from Tulane university:

At the end of the partitioning step, the variable i points to the pivot, everything to the left is less than 6, and everything to the right is bigger than 6. Now the pivot is in it’s final sorted position, and the left and right sub-arrays can be sorted independently. At this point, we can make two recursive calls on the left and right sub-arrays.

quicksort(numbers, start, pivot); // sort left sub-array
quicksort(numbers, pivot, end);   // sort right sub-array

This will create a binary tree of recursive function calls, until it bottoms out at sub-arrays with 0 or 1 element in them. That base case is handled by a conditional that only recurses if end - start > 2:

void quicksort(int numbers[], int start, int end) {
  if(end - start > 2) {
    int pivot = partition(numbers, start, end);
    <<<recurse>>>
  }
}

Define the partition function

In order to make the partition step fast, we want to avoid shifting the whole array around. A good way to do this is to swap elements in place.

void swap(int *a, int *b) {
  int temp = *a;
  *b = *a;
  *a = temp;
}

Now to the partition function, the i variable will be the upper bound of the left partition. The j variable will be the upper bound of the right partition. The pivot will be stored in the last position of the array, at index n-1. The region between j and (n-1)-1 is the unprocessed part of the array.

int partition(int numbers[], int start, int end) {
  int pivot = numbers[end];
  int i = start-1;
  for(int j = start; j < end-1; j++) {
    if(numbers[j] <= pivot) {
      i += 1;
      swap(&numbers[j], &numbers[i]);
    }
  }
  swap(&numbers[i+1], &numbers[end]); // Move pivot to between left and right
}

Define the input and read in unsorted numbers

Let’s name array to be sorted: numbers. Let n be the size of the unsorted array. For this program, I generated a list of 1,000,000 unsorted integers in this file: unsorted_integers.txt, they are newline-delimited. This code block defines the parameters and reads all the million integers into the numbers array.

int n = 1000000;
int numbers[n];
FILE *file = fopen("unsorted_integers.txt", "r");
for(int m = 0; m < n; m++) {
  fscanf(file, "%d\n", &numbers[m]);
}
fclose(file);

The main program

#include <stdio.h>  // for printf
#include <stdlib.h> // for FILE

<<<swap function>>>

<<<partition function>>>

<<<quicksort function>>>

int main(int argc, char *argv[]) {
  <<<read in unsorted numbers>>>
  return 0;
}