Notes on interest rates
This page is about interest rates, negative interest rates, and complex interest rates. I think interest rates are interesting because they represent the value of time.
Table of Contents
“Compound interest is the eighth wonder of the world. He who understands it, earns it … he who doesn’t … pays it.” ― Albert Einstein
This quote is special because Einstein revolutionized our understanding of time, and interest is intimately related to the value of time. The interest rate is frequently used to discount money in the future. Another cool way to think about interest is that it’s the price of sending money back in time.
Interest rates
In all of these notes, we assume that interest compounds. That means that interest is earned on interest, or from the other side of the transaction, interest is paid on interest.
The definition of an interest rate is a non-negative real number \( r \in [0, \infty) \). Call the principal \(P \in [0, \infty)\).
Then, if the interest compounds annually, after t years, the total value of the investment is $$ P(1 + r)^{t} $$
As an example, assume you bought a $1000 bond that earned 5% interest compounded annually. P = $1000 and r = 0.05, after 20 years, the value would be ($1000)*(1 + 0.05)20 = $2653.30
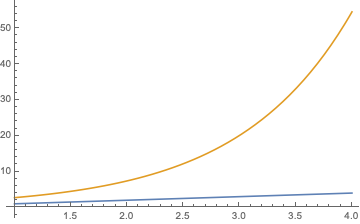
What about the really, really long term? How does the interest grow? Looking back at the formula:
$$ P(1 + r)^{t} $$
You can see that if the interest rate r is fixed over time, that it grows exponentially in t. This is what makes it ’the wonder of the world’. Saving $X dollars a year grows linearly, but interest compounds exponentially.
The Federal Reserve
The Federal Reserve is the central bank of the United States. It has a dual mandate to keep inflation low and also keep unemployment low. It’s main tool for doing this are “Open Market Operations”, which amount to buying bonds with newly printed money, or removing bonds from circulation. These buying and selling operations can guide the federal funds rate to the Federal Reserve’s goal. The federal funds rate is a minimum interest rate. If it’s low, then borrowing is cheap and unemployment will fall, since it’s cheaper for businesses to borrow and hire people. However, if it remains too low for too long, it’s possible that all that cheap borrowed money could push up inflation.
The Federal Reserve has to set the interest rate low enough to encourage job creation, but not too low that it stokes more inflation than the target.
The long-term decline of interest rates
The Bank of England published an interesting document called Eight centuries of global real interest rates, R-G, and the ‘suprasecular’ decline, 1311–2018. In it they find a -1.96bps (basis point, or 0.01%) per year trend. That means that for the last 800 years, real interest rates have been declining by -0.02% per year.
Negative interest rates
After the crash of 2008, central banks around the world lowered their interest rates to 0 in order to prevent the financial crash from turning into a repeat of the Great Depression. This worked in the United States, but in the European Union, the ECB (European Central Bank) had to experiment with lowering their interest rates to below 0.
What does a negative interest rate mean? It means that the banks pay you to borrow money. Similarly, it charges savers for keeping their money in the bank. As an example, a Danish bank offered negative interest rate mortgages. The whole purpose of negative interest rates is to encourage money to circulate, instead of staying in bank accounts.
So, \(r\) can be any real number, negative, positive or zero. What about complex numbers?
(For a primer on imaginary and complex numbers, see my post Imaginary Numbers are Real)
Complex interest rates
What would a complex interest rate mean? If you are comfortable with math, you might bust out the compound interest formula and just change them from being real variables to being complex variables. So, assume \(P, r \in \mathbb{C}\), the set of complex numbers. Then \(P = A + iB\) and \(r = c + id\), where \( A, B, c, d \in \mathbb{R} \).
Then \( P(1 + r)^{t} \) becomes
$$ (A + iB)(1 + (c + id))^{t} $$
But wait a minute, what does an imaginary amount of money mean? One way to imagine it is that the currency unit is actually a pair of units, like say, USD and DOGE. And there’s this rule that if you multiply 1 DOGE * 1 DOGE it becomes worth -1 USD. This is equivalent to the complex number arithmetic.
So all wallets in the economy would have US Dollars and Dogecoin, and the Federal Reserve would set the complex federal funds rate so that the compound interest grows in a spiral that doesn’t diverge too quickly.
One way to see it is to convert the complex number to polar coordinates, then raising it to a power will cause it to grow in a spiral or shrink in a spiral. Here’s an example I cooked up with Mathematica:

Update from 2021-10-12: When I wrote the first draft on 2021-09-09, I was unaware of any other attempt to define complex rates of return. I thought I had invented it, but I was wrong. Here’s a paper from 2010 called “The Simple Meaning of Complex Rates of Return”:
In Pierru 2010, the paper talks about the real and imaginary components representing two assets, A and B, with their own distinct rates of interest, ρA and ρB, and the imaginary unit i is interpreted as an exchange operator, exchanging some of A for B, or vice versa.
Then the paper defines a complex rate of return in terms of ρA and ρB, where the period over which the interest is accrued is followed by an exchange between asset A and B.
Ethereum smart contract implementing complex money: ComplexMoney on Repl.it